帰無仮説検定は，心理学における統計の利用シーンの代表的なものだろう。 その手順は形式化されており，統計パッケージによってはデータの種類を指定するだけで自動的に結果の記述までしてくれるものもあるほどである。誰がやっても同じ結果になり，また，機械的に手続きを自動化できることは大きな利点ではある。欠点は，初学者がそのメカニズムを十分に理解せずに誤った結果を得たり，悪意のある利用者が自分に都合の良い数字を出させたりすることにある。科学的営みは悪意をもった実践者を想定しておらず，もしそのような悪例が露見した場合には事後的に摘発・対処するしかない。しかし残念なことながら，初学者の浅慮や意図せぬ悪用も多くみられる。
心理学において，先行研究の結果が再現しないことを再現性問題というが，そのひとつは統計的手法の誤った使い方にあるとされる(池田 and 平石 2016)。改めて，丁寧に帰無仮説検定の手続きやロジックを見ていくことにしよう。
帰無仮説検定は，実験や調査で得たデータから得られた知見が意味のあるものかどうか，母集団の性質として一般化可能かどうかを判定するための枠組みである。手法と判断基準が明確なゲームの一種だと考えたよう。というのも，帰無仮説検定は有意水準という基準を設けて，帰無仮説と対立仮説という2つの考え方(モデル)を対決させ，勝敗を決するものだからである。勝敗を決するとしたのは，帰無仮説と対立仮説は排他的な関係にあるからであり，どちらも正しいとかどちらも間違っているという結末にはならないからである。ただし，あくまでも推測統計的なロジックに基づく判定であるから，判定結果にも確率的な要素が含まれる。本当は帰無仮説が正しい時に，間違って「対立仮説が正しい」と判定してしまう確率はゼロではない。逆に帰無仮説が正しくない時に，間違って「対立仮説が正しくない(帰無仮説が正しい)」と判定してしまう可能性もある。前者をタイプ1エラー，後者をタイプ2エラーという。どちらの確率もゼロであってほしいが，そうはならないので，前者を\(\alpha\)，後者を\(\beta\)としたときに，それぞれを一定の水準以下に抑えたい。この目的のために手順を整え，一般化したのが帰無仮説検定である。なお，先に述べた有意水準は，この\(\alpha\)の許容される水準であり，心理学では一般に5%に設定する。
このように帰無仮説検定という考え方は，エラーの統制が本来の狙いであるから，「有意になるように工夫する」という発想は根本的に間違っている。また，統計的推定という数学的手続きに，人間が納得しやすい判定を下すという人為的手続きが組み合わさったものであるから，帰無仮説検定の結果に過剰な意味を持たせたり一喜一憂したりすることがないように注意しよう。
帰無仮説検定の手続きを一般化すれば，次のようになる。
帰無仮説検定は，群間の平均値に差があるかどうか，相関係数に統計的な意味があるかどうかといった事例に対して適用される。 当然のことながら，これは標本から母集団を推定するという文脈における話で，物理学的な真偽を理論的に判断するとか，全数調査のように母集団全体の情報が手に入る場合といった場合の話ではない。また，標本のサンプルサイズが小さく，標本統計量の信頼区間が大きいことから，枠組みなしには判定できないという背景があることも再確認しておこう。
母集団の状態がわからないので，仮説を設定する。帰無仮説Null Hypothesisは空っぽの仮説という意味で，母平均差がない(差がゼロ，\(\mu_1 - \mu_2 = 0\))とか，母相関がゼロ(\(\rho = 0\))である，とされる。対立仮説Alternative Hypothesisは帰無仮説と排他的な関係にある仮説としてつくられるから，「差が無くはない(\(\mu_1 - \mu_2 \neq 0\))」「相関がゼロではない(\(\rho \neq 0\))」という表現になる。なぜ帰無仮説がゼロであることから始められるかといえば，ふたつの排他的な仮説を考えた時にゼロでない状態というのは無数にあり得るので，仮説として特定できないからである(差が1のとき，1.1のとき，1.11のとき・・・と延々と検定し続けるわけにもいくまい)。
検定統計量の選択は，二群の平均値差のときは\(t\)，三群以上の時は\(F\)，相関係数の検定も\(t\)，と天下り的に示されることが一般的である。もちろんこれらの統計量が選ばれるのは，数理統計的な論拠に基づいている。判定基準は5%水準とすることが一般的だし，検定統計量の計算はアルゴリズムに沿って機械的に可能である。判定は客観的な指標に基づいて行われるから，「どの状況でどのような帰無仮説をおくか」が類型化できれば，この手続き全体が自動的に進められる。
しかしここでは改めて，丁寧に手順を追いながらみてみよう。
ここでは相関係数の検定を例に取り上げる。俗に「無相関検定」と呼ばれるように，相関がどれほど大きいとかどれほど意味があるということをチェックするのでは無く，無相関ではない，ということをチェックする。もちろん標本相関は計算してゼロでなければ，それは無相関ではない。ここで考えたいのは，母相関がゼロではないということである。言い換えると，母相関がゼロの状態であっても，標本相関がゼロでないことは，小標本のサンプリングという背景のもとでは当然のことである。
確認してみよう。まず，無相関なデータセットを作ることを考える。RのMASSパッケージを使い，多変量正規分布の確率分布関数から乱数を生成しよう。
library(MASS)
set.seed(12345)
N <- 100000
X <- mvrnorm(N,
mu = c(0, 0),
Sigma = matrix(c(1, 0, 0, 1), ncol = 2),
empirical = TRUE
)
head(X) [,1] [,2]
[1,] -0.4070308 -0.72271139
[2,] -0.5774631 -0.57075167
[3,] 0.2312929 -0.42458994
[4,] 0.6242499 -0.55522146
[5,] -0.7791585 0.55004824
[6,] 1.8995860 -0.04899946ここでは10^{5}個の乱数を生成した。つくられたオブジェクトXは表示されているように，2変数からなる。ここでは相関のある2変数を想定しており，各変数がそれぞれ標準正規分布に従っているという設定である。rnorm関数を2つ使って2変数をつくっても良いのだが，2変数セットで取り出すことを考えると多変量正規分布をかんがえることになる。多変量正規分布は，ひとつひとつの変数については正規分布として平均とSDをもち，かつ，変数の組み合わせとして共分散をもつものである。mvrnormの引数をみると，muは平均ベクトルであり，Sigmaが分散共分散行列である。分散共分散行列とは，ここでは\(2\times 2\)の正方行列であり，対角項に分散を，非対角項に共分散をもつ行列である。共分散は標準偏差と相関係数の積で表される。
分散
\[ s_x^2 = \frac{1}{n}\sum (x_i - \bar{x})^2 = \frac{1}{n}\sum (x_i - \bar{x})(x_i - \bar{x})\]
標準偏差
\[ s_x = \sqrt{s_x^2} = \sqrt{\frac{1}{n}\sum (x_i - \bar{x})^2}\]
共分散
\[ s_{xy} = \frac{1}{n}\sum (x_i - \bar{x})(y_i - \bar{y})\]
相関係数
\[r_{xy} = \frac{s_{xy}}{s_xs_y} = \frac{\frac{1}{n}\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\frac{1}{n}\sum (x_i - \bar{x})^2}\sqrt{\frac{1}{n}\sum (y_i - \bar{y})^2}}\]
分散共分散行列
\[\Sigma = \begin{pmatrix} s_x^2 & s_{xy} \\ s_{yx} & s_y^2 \end{pmatrix} = \begin{pmatrix} s_x^2 & r_{xy}s_xs_y \\ r_{xy}s_xs_y & s_y^2 \end{pmatrix}\]
今回Sigma = matrix(c(1,0,0,1),ncol = 2)としたのは，この2変数が無相関であること(SDはそれぞれ1であること)を指定している。ちなみにempirical = TRUEのオプションは，生成された乱数が設定した分散共分散行列のもつ相関係数と一致するように補正することを意味している。
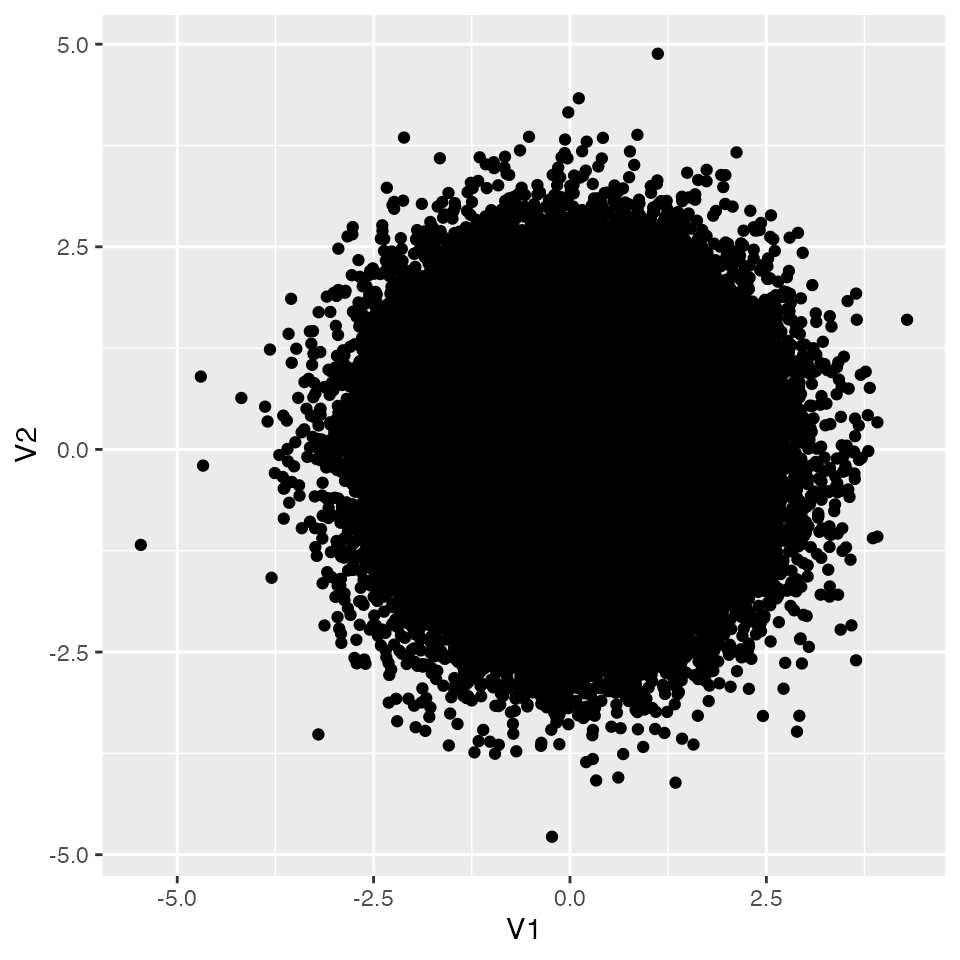
可視化しておこう。つくられた乱数が無相関であることを，散布図を使って確認する。
library(tidyverse)── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
✖ dplyr::select() masks MASS::select()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsX %>%
as.data.frame() %>%
ggplot(aes(x = V1, y = V2)) +
geom_point()
数値的にも確認しておこう。
cor(X) %>% round(5) [,1] [,2]
[1,] 1 0
[2,] 0 1つくられた乱数が無相関であることが確認できた。さてこれが母集団であったとして，ここからたとえばn = 20のサンプルをとったとする。この時の相関はどうなるだろうか。 Rで計算してみよう。sample関数をつかって抜き出す行を決めて，該当する行だけs1オブジェクトに代入する。その上で相関係数を計算してみよう。
selected_row <- sample(1:N, 20)
print(selected_row) [1] 9647 80702 57543 93179 99032 82624 32672 53670 69698 42383 23801 69303
[13] 9816 61803 69464 23107 76958 44447 10 27292s1 <- X[selected_row, ]
cor(s1) [,1] [,2]
[1,] 1.0000000 0.1431698
[2,] 0.1431698 1.0000000今回の相関係数は0.1431698となった。母集団の相関係数が0であっても，適当に抜き出した20点が相関係数を持ってしまう(0でない)ことはあり得ることなのである。問題は，これがどの程度あり得ることなのか，である。いいかえると，研究者が\(n=20\)のサンプルをとって相関を得た時，それが\(r = 0.14\)であったとしても，母相関\(\rho = 0.0\)からのサンプルである可能性がどれぐらいあるか，ということである。
標本相関係数は確率変数なので，毎回標本を取る度に値が変わるし，どの実現値がどの程度出現するかは標本分布で表現できる。 ではどのような標本分布に従うのだろうか。先ほどのサンプリングを繰り返して，乱数によって近似してみよう1。
iter <- 10000
samples <- c()
for (i in 1:iter) {
selected_row <- sample(1:N, 20)
s_i <- X[selected_row, ]
cor_i <- cor(s_i)[1, 2]
samples <- c(samples, cor_i)
}
df <- data.frame(R = samples)
# ヒストグラムの描画
g <- df %>%
ggplot(aes(x = R)) +
geom_histogram(binwidth = 0.01)
print(g)
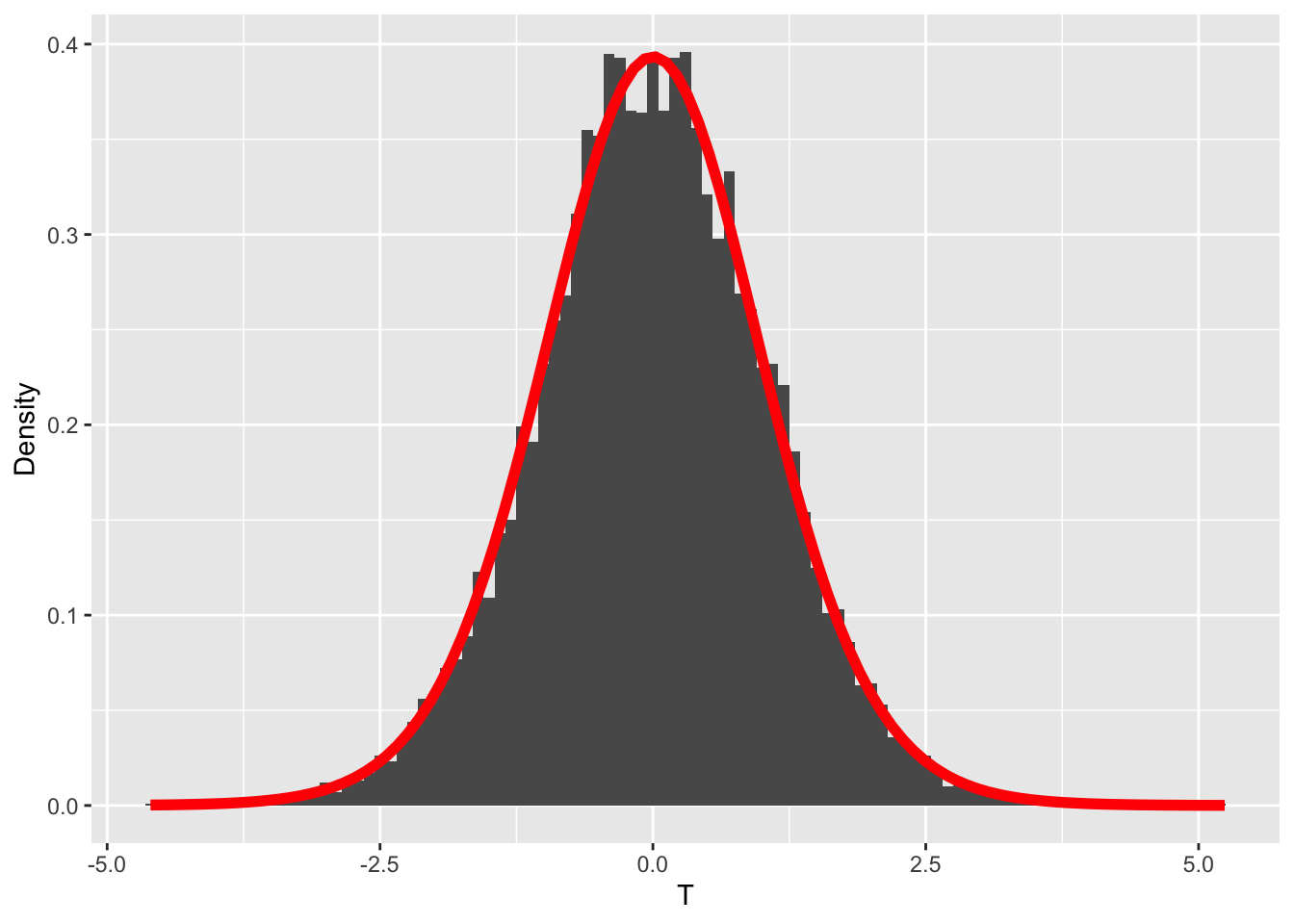
ヒストグラムを見ると，サンプルサイズが20の場合，母相関係数\(\rho = 0.0\)であっても\(r = 0.3\)や\(r=0.4\)程度の標本相関が出現することはある程度みられることである。
また，標本分布は左右対称の何らかの理論分布に従っていそうだ。数理統計学の知見から，相関係数の場合，標本相関係数を次の式によって変換することで，自由度が\(n-2\)の\(t\)分布に従うことが知られている。
\[ t = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} \]
df %>%
mutate(T = R * sqrt(18) / sqrt(1 - R^2)) %>%
ggplot(aes(x = T)) +
geom_histogram(aes(y = after_stat(density)), binwidth = 0.1) +
# 自由度18のt分布の確率密度関数を追加
stat_function(fun = dt, args = list(df = 18), color = "red", linewidth = 2) +
# Y軸のラベルを変更
ylab("Density")
これを利用して相関係数の検定が行われる。以下，サンプルサイズ20で標本相関係数が\(r=0.5\)だったとして，手順に沿って解説する。
(1 - pt(0.5 * sqrt(18) / sqrt(1 - 0.5^2), df = 18)) * 2[1] 0.02476956qt(0.975, df = 18)[1] 2.100922ここで注意してほしい点は，今回の検定の目的が「母相関が0であるという帰無仮説を棄却できるかどうか」であり，相関係数の符号については関心がなく絶対値で考える点である。pt関数は，ある確率点までの累積面積であるから，1から引くことでその確率点以上の値がでる確率が示される。\(t\)分布は左右対称の分布なので，これを2倍した値が絶対値で考えた時の出現確率である。これが5%よりも小さければ，有意であると判断できる。今回は，統計的に有意であるといって良い。
なお，表現上の細かい注意点になるが，この確率は今回の実現値「以上」のより極端な値が出る確率であり，この実現値が出る確率という言い方はしない。確率は面積であり，点に対する面積はないからである。
qt関数で示されるのは確率点なので，これ以上の値を今回の実現値が出していたら，統計的に有意であると判断できる。今回の実現値から算出した値は\(t(18)=2.449\)であり，臨界値の\(2.100\)よりも大きな値なので，有意であると判断できる。
上では丁寧に計算過程をみてきたが，実践場面ではサンプルはひとつであり，標本統計量もひとつ算出されるだけである。自分の大切なデータであるから，標本分布から得られた特定のケースにすぎないことが直感的にわかりにくいかもしれない。
相関係数の検定をするときは，Rの関数cor.testを使って次のように行う。ここではmvrnorm関数を使って，相関係数0.5の仮想データを作っている。
set.seed(17)
n <- 20
sampleData <- mvrnorm(n,
mu = c(0, 0),
Sigma = matrix(c(1, 0.5, 0.5, 1), ncol = 2),
empirical = TRUE
)
cor.test(sampleData[, 1], sampleData[, 2])
Pearson's product-moment correlation
data: sampleData[, 1] and sampleData[, 2]
t = 2.4495, df = 18, p-value = 0.02477
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.07381057 0.77176071
sample estimates:
cor
0.5 結果として示されている，tの値や自由度，\(p\)値が先ほど示した例と対応していることを確認できる。さらに，相関係数の信頼区間や標本相関係数そのものも示されている。この信頼区間が0を跨いでいないことからも，帰無仮説が棄却されることが見て取れるだろう。
われわれは既に，母相関が0のデータセットの一部を取り出すと，その相関係数が0ではなく0.5のような数字になることも知っている。もちろん母相関が0であれば標本相関も0近い値が出やすいとしても，である。つまり標本から得られた値をあまり大事に考えすぎない方が良い(もちろん一般化を念頭においている時は，である)。 また，帰無仮説は「母相関が0である」なので，これが棄却されたとしても「母相関が0であるとは言えない」のに過ぎない。ここから，母相関も\(r=0.5\)付近にあるはずだとか，\(p\)値が2.4%なので5%よりもずいぶん低いのは証拠の重要さを物語っているのだ，と論じるのは適切ではない。母相関が0という仮想的な状況のもとでの話であって，母相関が実際にどの程度なのかを検討しているわけではない。この点が誤解されやすいので特に注意してほしい。
ここに来るとタイプ1エラー，タイプ2エラーがより具体的に理解できるようになってきたではないだろうか。タイプ1エラーはこの帰無仮説が正しい時に，標本相関から計算した統計量で判断する確率であるから，上の手続きで見たことそのものである。
別の角度で見てみよう。cor.testをつかうと標本統計量の信頼区間が算出できる。この信頼区間が母相関–ここでは帰無仮説である\(\rho =0\)を「正しく」含んでいる割合を見てみよう。 cor.test関数が返すオブジェクトには，conf.intという名前のものがあり，デフォルトではここで95%の信頼区間が含まれている。 シミュレーションに先立って，結果を格納する2列のデータフレームを作っておき，シミュレーション後にifelse関数で母相関が含まれているかどうかの判定をした。
set.seed(42)
iter <- 10000
intervals <- data.frame(matrix(NA, nrow = iter, ncol = 2))
names(intervals) <- c("Lower", "Upper")
for (i in 1:iter) {
selected_row <- sample(1:N, 20)
s_i <- X[selected_row, ]
cor_i <- cor.test(s_i[, 1], s_i[, 2])
intervals[i, ] <- cor_i$conf.int[1:2]
}
#
df <- intervals %>%
mutate(FLG = ifelse(Lower <= 0 & Upper >= 0, 1, 0)) %>%
summarise(type1error = mean(FLG)) %>%
print() type1error
1 0.95今回の例では，95%の割合で正しく判断できていた。言い換えると，エラーが生じる割合は5%だったので，タイプ1エラー確率を5%以下にするという目的はしっかり達成できていたことが確認できた。
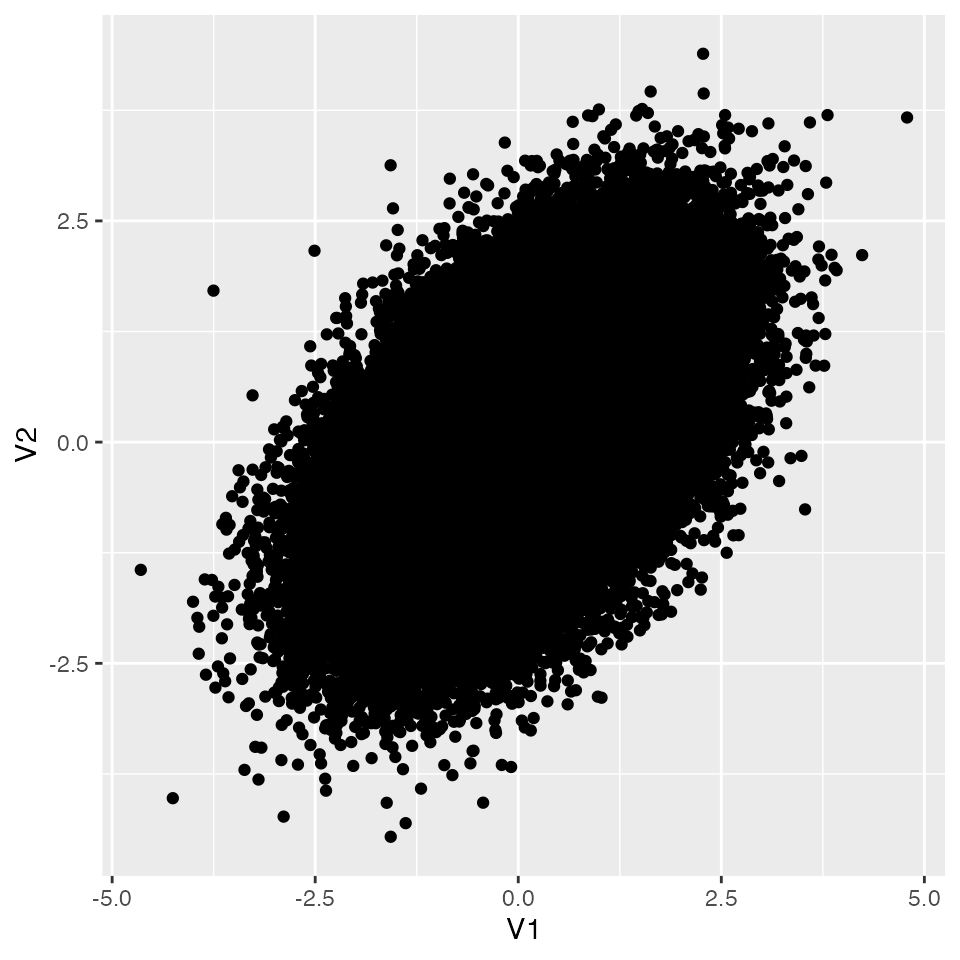
同様に，タイプ2エラーは，帰無仮説が正しくないときに帰無仮説を採択する確率だから，シミュレーションするなら次のようになる。まず母相関が0でない状況を作り出そう。今回は母相関が0.5であるとして，母集団分布を描いてみよう。
set.seed(12345)
N <- 100000
X <- mvrnorm(N,
mu = c(0, 0),
Sigma = matrix(c(1, 0.5, 0.5, 1), ncol = 2),
empirical = TRUE
)
X %>%
as.data.frame() %>%
ggplot(aes(x = V1, y = V2)) +
geom_point()
今度は，ここからサンプルサイズ20のデータセットを取り出し，検定することにしよう。検定の結果，有意になれば1，ならなければ0というオブジェクトを作って，判定の正しさを考えてみることにする。
iter <- 10000
judges <- c()
for (i in 1:iter) {
selected_row <- sample(1:N, 20)
s_i <- X[selected_row, ]
cor_i <- cor.test(s_i[, 1], s_i[, 2])
judges <- c(judges, cor_i$p.value)
}
df <- data.frame(p = judges) %>%
mutate(FLG = ifelse(p <= 0.05, 1, 0)) %>%
summarise(
sig = sum(FLG == 1),
non.sig = sum(FLG == 0),
type2error = non.sig / iter
) %>%
print() sig non.sig type2error
1 6442 3558 0.3558今回は母相関が0.5であり，帰無仮説は棄却されて然るべきなのだが，有意でないと判断された割合が35.58%あったことになる。心理学の研究などでは，この確率\(\beta\)が0.2未満，逆にいうと検出が0.8以上あることが望ましいとされているので，今回のこの事例では十分な件出力がなかった，と言えるだろう。
もちろん実際には，母相関がどれぐらいなのかわからない。\(0.3\)なのかもしれないし，\(-0.5\)であるかもしれない。つまりタイプ2エラーは研究者が制御できるところではなく，せいぜい大きな相関が見込めそうな変数について標本を取ろうと心がけるだけである。
タイプ1,2エラーの確率は，サンプルサイズや効果量(ここでは母相関の大きさ)の関数である。サンプルサイズは研究者が決定することができるので，効果を見積もり，制御したいエラー確率の基準を決めて，合理的にサンプルサイズを決めるべきである。
cor.test をつかって検定し，検定結果と判断結果を記述してください。cor.testを使って検定し，検定結果を一覧にしてみましょう。ここから何がわかるでしょうか。このような二度手間を取らず，mvrnormからサンプルサイズ20の乱数を反復生成しても良い。母集団を具体的なものとしてイメージするために，母相関が0の母集団からサンプリングを繰り返す方法をとった。↩︎