ここでは回帰分析を扱う。説明変数\(x\)と被説明変数\(y\)の関数関係\(y=f(x)\)に，次の一次式を当てはめるのが単回帰分析である。
\[ y_i = \beta_0 + \beta_1 x_i + e_i = \hat{y}_i + e_i\]
一次式を\(\hat{y}\)とまとめたものを予測値といい，予測値と実測値\(y\)の差分\(e_i\)を残差residualsという。
空間上の一次直線の切片，傾きを求めるというのが基本的な問題であり，二点であれば一意に定めることができるが，データ分析の場面では3点以上の多くのデータセットの中に直線を当てはめることになるので，なんらかの外的な基準が必要になる。この時，「残差の分散が最も小さくなるように」と考えるのが最小二乗法の考え方であり，「残差が正規分布に従っていると考え，その尤度が最も大きくなるように」と考えるのが最尤法の考え方である。前者は記述統計的な，後者は確率モデルとしての感が過多になっていることに注意してほしい。また確率モデルの推定方法としては，事前分布を用いたベイズ推定が用いられることもある。
最小二乗法による推定値は，次の式で表される。証明は他書(小杉 2018; 西内 2017)に譲るが，ロジックとして残差の二乗和\(\sum e_i^2 = \sum (y_i - (\beta_0 + \beta_1 x_i))^2\)を最小にすることを考え，この式を展開するか偏微分を用いて極小値を求めることで算出できるとだけ伝えておこう。いずれにせよ，平均値\(\bar{x},\bar{y}\)や分散・共分散\(s_x,s_y,r_{xy}\)など標本統計量から推定できるのはありがたいことである。
\[\beta_0 = \bar{y} - \beta_1\bar{x},\quad \beta_1 = r_{xy} \frac{s_y}{s_x}\]
また，ここでは\(x,y\)ともに連続変数を想定しているが，説明変数\(x\)が二値，あるいはカテゴリカルなものであれば\(y\)の平均値を通る直線を探すことになる。直線の傾きが0であれば「平均値が同じ」という線形モデルであり，これは平均値差の検定における帰無仮説と同等である。このように，t検定やANOVAは回帰分析の特殊ケースとも考えられ，まとめて一般線形モデルと呼ばれる。一般線形モデルは，被説明変数が連続的で，線形モデルによる平均値に正規分布に従う残差が加わったものとして考えるという意味で統一的に表現される。
ANOVAの場合は，二つ以上の要因による効果を考えることもあった。交互作用項を考慮しなければ，2要因のモデルは次のように表現することができる。
\[ y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + e_i \]
このように説明変数が複数ある回帰分析を特に重回帰分析Multiple Regression Analysisと呼ぶ。一次式なので，ある変数に限れば線形性が担保されているから，これも線形モデルの仲間である。重回帰分析を用いる場合は，説明変数同士を比較して「どちらの説明変数の方が影響力が大きいか」ということが論じられることが多いが，係数は当然\(x_n, y\)の単位に依存するため，素点の回帰係数は使い勝手が悪い。そこですべての変数を標準化した標準化係数が用いられることが多い。
以下，具体的なデータを用いて回帰分析の特徴を見てみよう
回帰分析のモデル式にそってデータを生成し，分析によってパラメータリカバリを行ってみよう。
説明変数については制約がないので一様乱数から生成し，平均0，標準偏差\(\sigma\)の誤差とともに被説明変数を作り，
library(tidyverse)
set.seed(123)
n <- 500
beta0 <- 2
beta1 <- 3
sigma <- 1
# データの生成
x <- runif(n, -10, 10)
e <- rnorm(n, 0, sigma)
y <- beta0 + beta1 * x + e
dat <- data.frame(x, y)
# データの確認
head(dat) x y
1 -4.248450 -11.120952
2 5.766103 18.736432
3 -1.820462 -3.805302
4 7.660348 25.071541
5 8.809346 30.026546
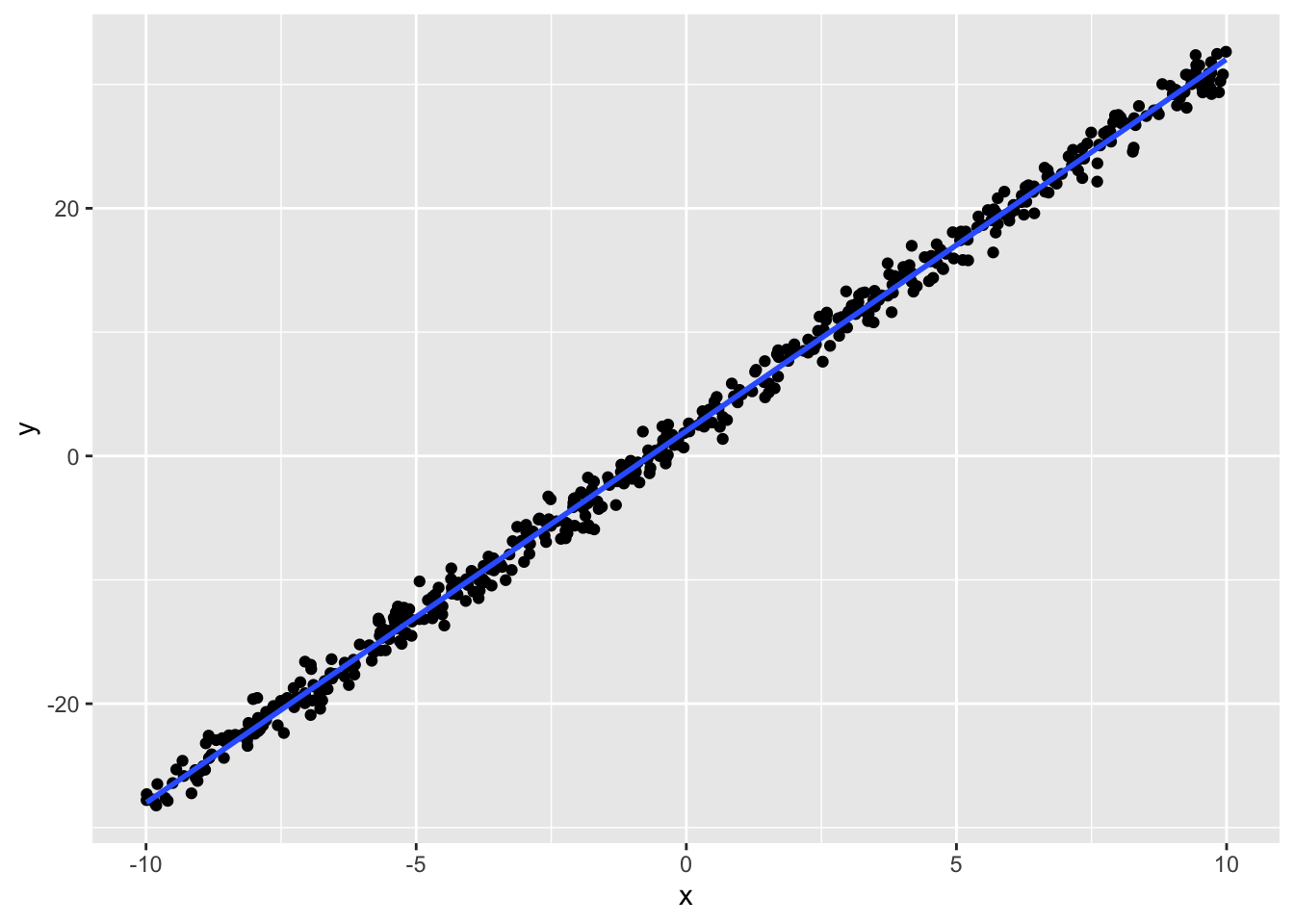
6 -9.088870 -25.355175dat %>% ggplot(aes(x = x, y = y)) +
geom_point() +
geom_smooth(method = "lm", formula = "y~x") # 線形モデルの描画
このデータに基づいて回帰分析を実行した結果が以下のとおりである。
result.lm <- lm(y ~ x, data = dat)
summary(result.lm)
Call:
lm(formula = y ~ x, data = dat)
Residuals:
Min 1Q Median 3Q Max
-2.82796 -0.61831 0.03553 0.69367 2.68062
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.021928 0.045010 44.92 <2e-16 ***
x 3.002194 0.007919 379.09 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.006 on 498 degrees of freedom
Multiple R-squared: 0.9965, Adjusted R-squared: 0.9965
F-statistic: 1.437e+05 on 1 and 498 DF, p-value: < 2.2e-16ここでは\(\beta_0 =2, \beta_1=3, \sigma = 1\)と設定しており，ほぼ理論通りの係数がリカバリーできていることを出力から確認しておこう。 もちろんリカバリの精度は，データの線形性の強さに依存するから，残差の分散が大きかったりサンプルサイズが小さくなると，必ずしもうまくリカバリできないことがあることは想像に難くないだろう。
lm関数が返した結果オブジェクトには，表示されていない多くの情報が含まれている。例えば予測値や残差も含まれているので，これを使って回帰分析の特徴を見てみよう。
dat <- bind_cols(dat, yhat = result.lm$fitted.values, residuals = result.lm$residuals)
summary(dat) x y yhat residuals
Min. :-9.99069 Min. :-28.216 Min. :-27.9721 Min. :-2.82796
1st Qu.:-5.08007 1st Qu.:-13.074 1st Qu.:-13.2294 1st Qu.:-0.61831
Median :-0.46887 Median : 0.301 Median : 0.6143 Median : 0.03553
Mean :-0.09433 Mean : 1.739 Mean : 1.7387 Mean : 0.00000
3rd Qu.: 4.65795 3rd Qu.: 15.963 3rd Qu.: 16.0060 3rd Qu.: 0.69367
Max. : 9.98809 Max. : 32.638 Max. : 32.0081 Max. : 2.68062 予測値\(\hat{y}\)はfitted.valuesとして保存されている。これの平均値が被説明変数\(y\)の平均値に一致していることが確認できる。回帰分析は説明変数\(x\)を伸ばしたり(\(\beta_1\)倍する)ズラしたり(\(\beta_0\)を加える)しながら，被説明変数\(y\)に当てはめるのであり，位置合わせがなされた予測値の中心が被説明変数の中心と一致することは理解しやすいだろう1。
次に，残差の平均が0になっていることも確認しておこう。これが0でない\(c\)であれば，回帰係数が常に\(c\)だけズレていることになるので，そのような系統的ズレは最適な線形の当てはめにおいて除外されているべきだからである2。
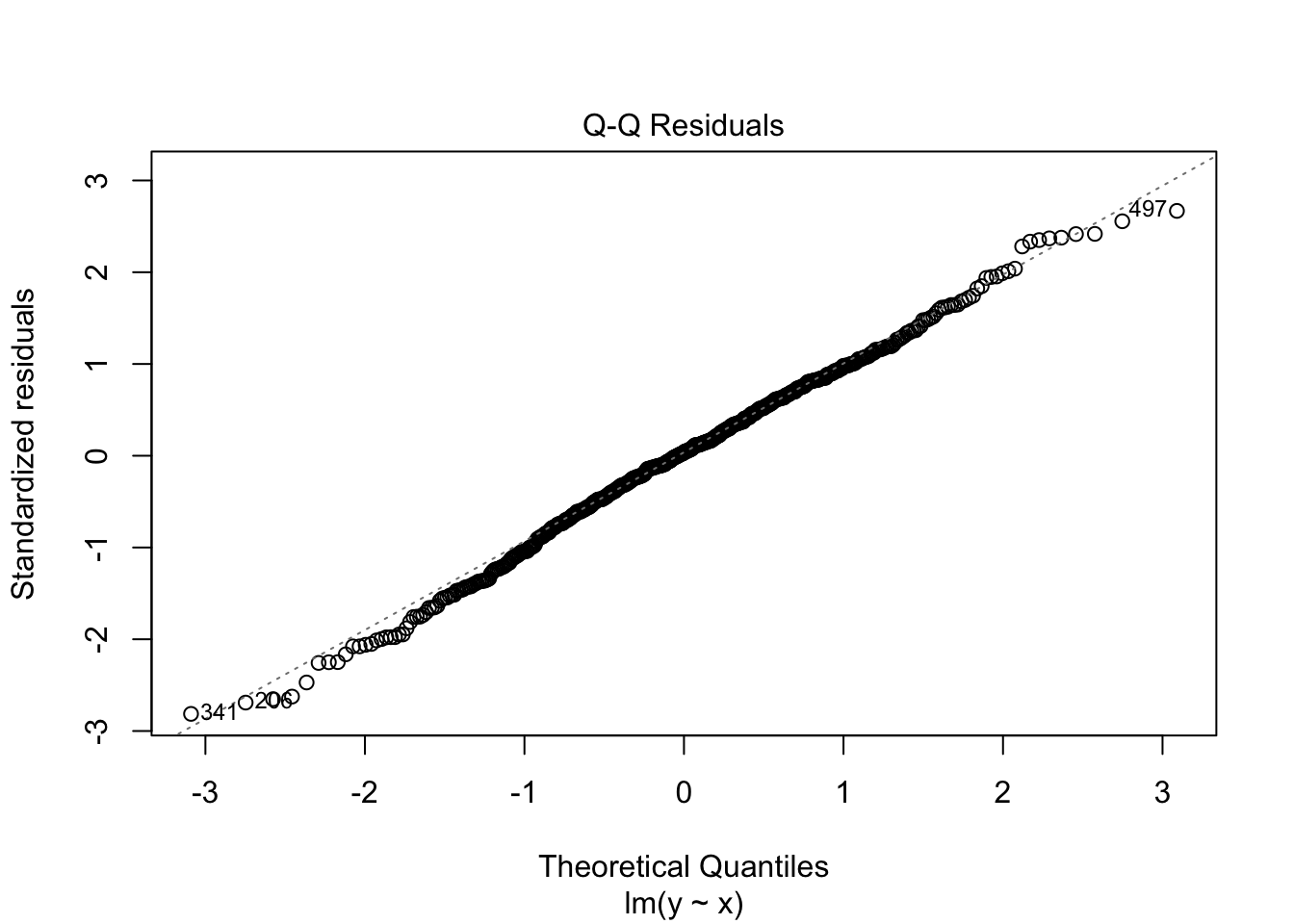
また，回帰分析において残差は正規分布に従うことが仮定されていた。これを検証するにはQ-Qプロットを見ると良い。
dat %>%
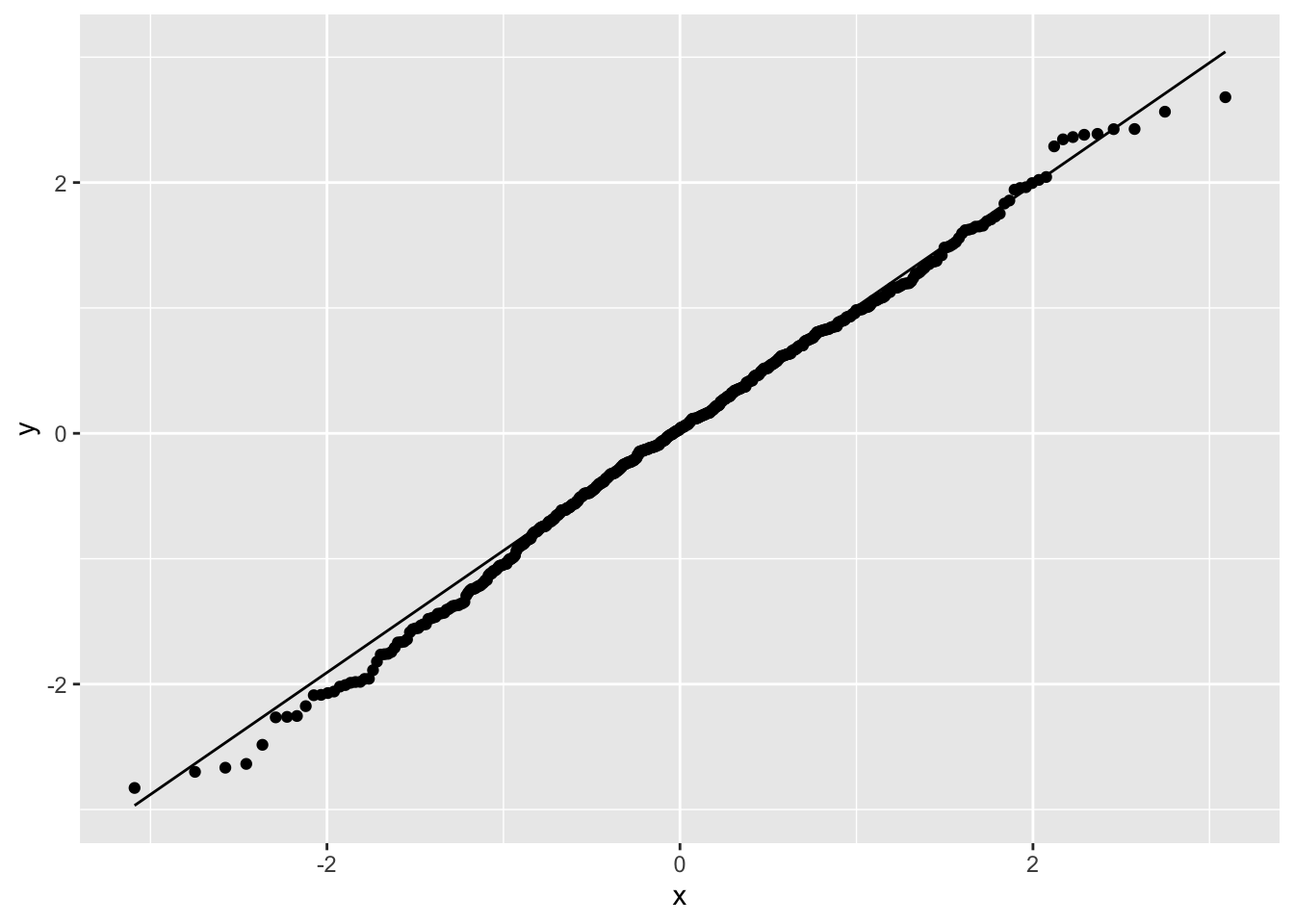
ggplot(aes(sample = residuals)) +
stat_qq() +
stat_qq_line()
Q-Qプロットとは2つの確率分布を比較するためのグラフであり，横軸には理論的分布の分位点が，縦軸に実データが並ぶもので，右上がりの直線上にデータが載っていれば分布に従っている，と判断するものである。直線から逸脱している点は理論的分布からの逸脱と考えられる。今回の結果はほとんどが正規分布の直線上にあることから，大きな逸脱がないことが認められる。
データ生成メカニズムによっては，被説明変数が二値的であったり，順序的であったり，カウント変数であったり，と正規分布がそぐわないものもあるだろう。そのようなデータに無理やり回帰分析を当てはめることは適切ではない。いかなる時もデータは可視化して，モデルを当てはめることの適切さをチェックすることを忘れたはならない。
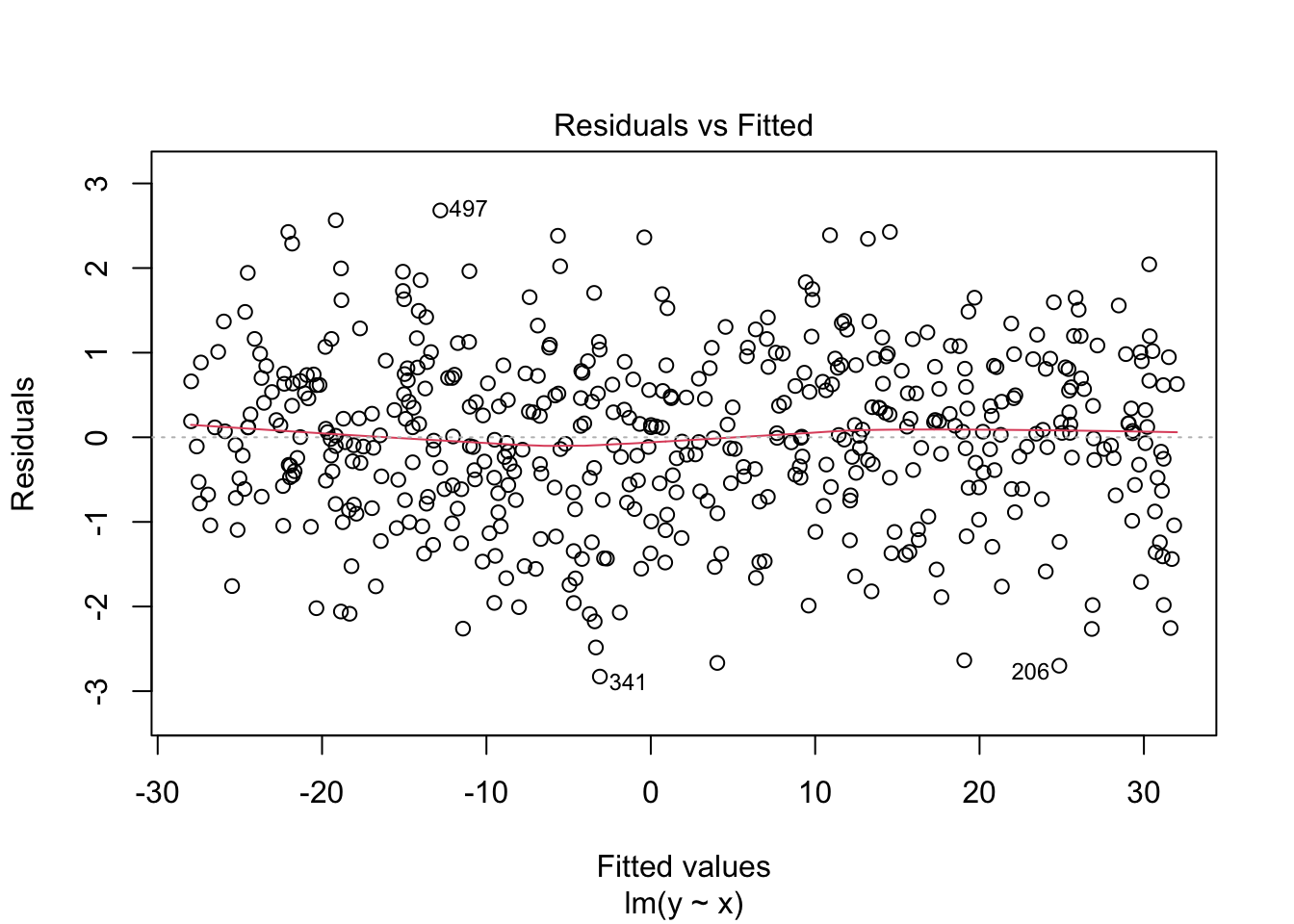
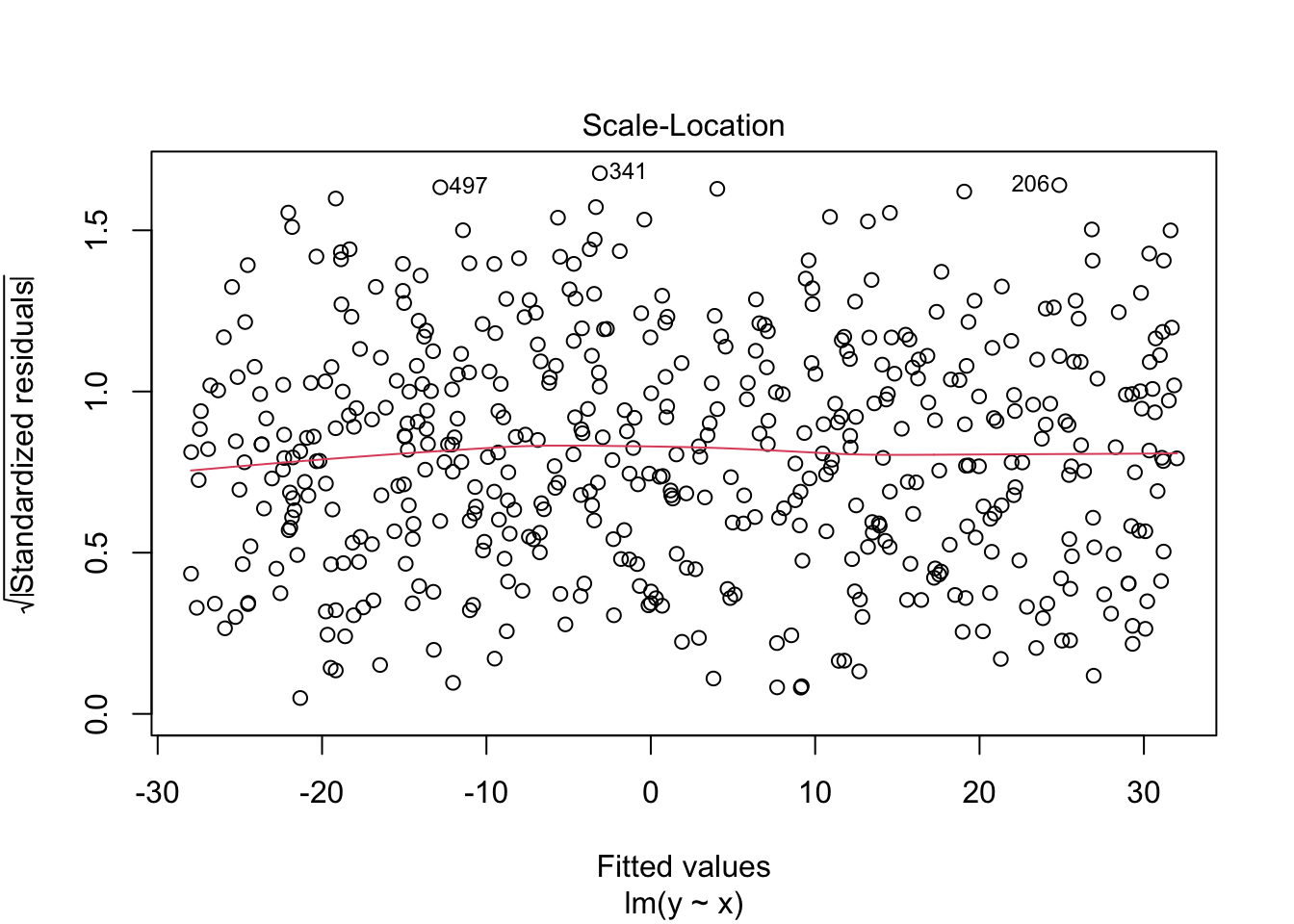
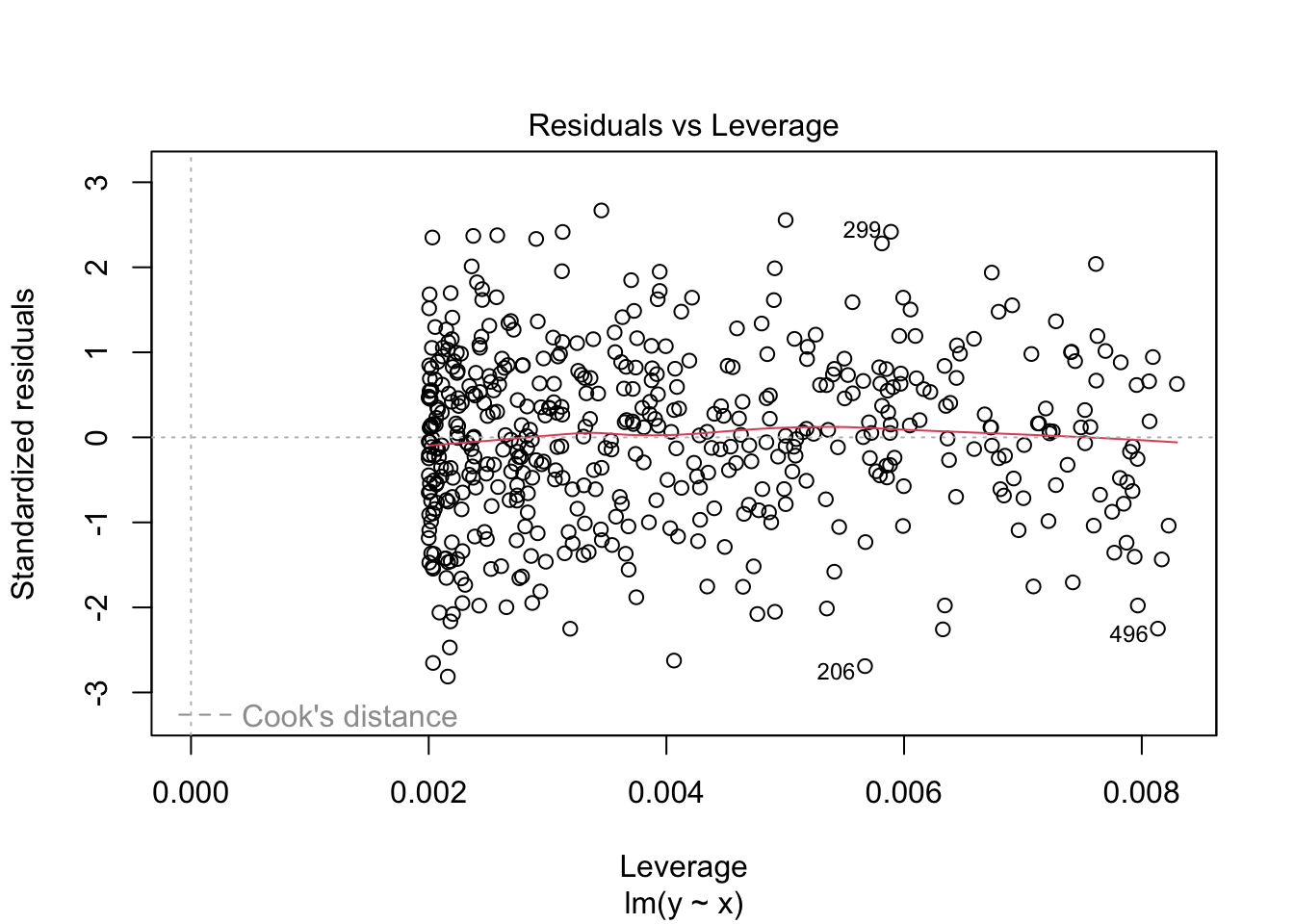
ちなみに出力結果を直接plot関数に入れてもよい。ここから残差と予測値の相関関係や，Q-Qプロット，標準化残差のスケールロケーションプロット，レバレッジと標準化残差3 などがプロットされる。
plot(result.lm)
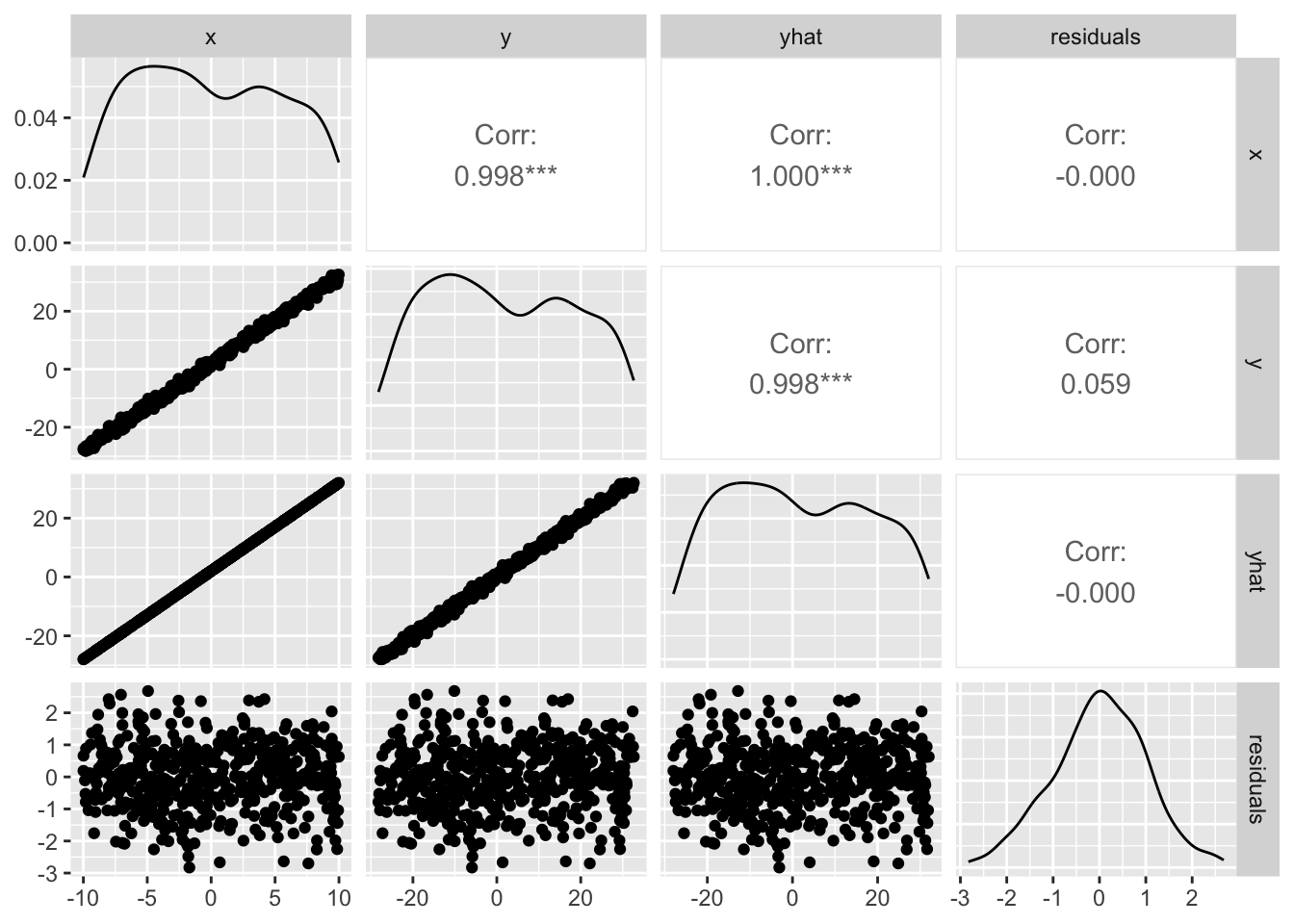
残差と予測値のプロットからも想像できるが，両者の相関はゼロである。図で確認しておこう。
library(GGally) # 必要ならインストールしよう
ggpairs(dat)
この関係から明らかなように，残差は説明変数や予測値と相関しない4。説明変数と残差に相関関係があるとすると，説明変数でまだ説明できていない分散が残っていることになるし，予測値と残差に相関がないことは予測値が高いか低いかにかかわらず，残差が一様に分布していることを意味する。このことを踏まえて，重回帰分析の特徴を理解していこう。
重回帰分析においては，回帰係数は偏回帰係数partial regression coefficientsと呼ばれる。この「偏」の一文字が意味することを考えていこう。
単回帰分析の回帰係数は，説明変数\(x\)が一単位上昇した時の被説明変数の変化量，と解釈すればよい。これに対して重回帰分析の偏回帰係数を，「説明変数\(x_1\)が一単位上昇した時の被説明変数の変化量」とすることはできない。というのも，説明変数が複数(\(x_2,x_3,\ldots\))あり，他の説明変数の次元についての変化を考慮していない変化量になっているからである。
重回帰分析において，説明変数が完全に無相関で直交しているのであれば，\(x_1\)の変化と\(x_2\)の変化を独立して説明できるが，往々にしてそのようなことはない。偏回帰係数は当該変数以外の変動を統制した回帰係数である。
上で単回帰係数において，説明変数と残差が相関しないことを確認した。言い換えれば，説明変数で説明でき分散は全て説明し尽くされており，残差は説明変数で説明できない被説明変数の分散，つまり説明変数の影響を除外した被説明変数の分散と考えることができる(被説明変数の分散=説明変数が説明する分散+残差の分散)。
ここで第二の変数\(x_2\)があったとする。第一の変数\(x_1\)で\(y\)を説明した残差\(e_y\)と，第一の変数で第二の変数を説明した残差\(e_{x2}\)との相関を偏相関partial correlationという。これは第一の変数\(x_1\)からの影響を両者から取り除いているので，\(x_1\)で統制した相関係数ということができる。偏相関は単純な相関が「見せかけの関係」でないことを検証するための重要な指標である。
偏相関係数を計算してみよう。
library(MASS)
library(psych)
Sigma <- matrix(c(1, 0.3, 0.5, 0.3, 1, 0.8, 0.5, 0.8, 1), ncol = 3)
X <- mvrnorm(1000, c(0, 0, 0), Sigma, empirical = TRUE) %>% as.data.frame()
## 相関行列
cor(X) V1 V2 V3
V1 1.0 0.3 0.5
V2 0.3 1.0 0.8
V3 0.5 0.8 1.0## 回帰分析をして残差を求める
result.lm1 <- lm(V2 ~ V1, data = X)
result.lm2 <- lm(V3 ~ V1, data = X)
cor(result.lm1$residuals, result.lm2$residuals)[1] 0.7867958## 偏相関を求めるR関数で確認
psych::partial.r(X)[2, 3][1] 0.7867958最後はpsychパッケージの偏相関行列を求める関数で検証した。確かに残差同士の相関係数が偏相関係数になっていることが確認できたと思う。
そして，ここでは残差同士の相関係数として算出しているが，残差をつかった回帰分析の係数が偏回帰係数になるのである。このデータセットの第一変数を従属変数にした重回帰分析の結果から，これを確認してみよう。
result.mra <- lm(V1 ~ V2 + V3, data = X)
# 回帰係数を取り出す
result.mra$coefficients (Intercept) V2 V3
-3.414371e-17 -2.777778e-01 7.222222e-01 # 残差をつかって偏回帰係数を確認する
result.lm3 <- lm(V1 ~ V3, data = X)
result.lm4 <- lm(V2 ~ V3, data = X)
result.lm5 <- lm(result.lm3$residuals ~ result.lm4$residuals)
#
result.lm5$coefficients (Intercept) result.lm4$residuals
3.242857e-17 -2.777778e-01 重回帰分析の結果result.mraのV2からV1への回帰係数は-0.2778である。また，V3でV1,V2を統制した残差同士をつかい，回帰係数を求めた結果は-0.2778と，同じ値になっていることが確認できただろう。
V3からV1への偏回帰係数も同様で，V2で両者を統制した残差同士による回帰係数になっている。このように，重回帰分析の回帰係数は，他の説明変数で統制した値になっており，日本語で説明するなら「他の変数の値が同じであると想定した条件つきの，当該変数の影響力」とでもいうべき値になっている。
なぜこのような持って回った説明をするかというと，つい「条件付きの」という話を忘れて報告，解釈してしまうことが多いからで，吉田 and 村井 (2021) の論文での指摘は議論を呼んだのは記憶に新しい5。 たとえば今回の例でも，回帰係数が-0.2778であったのに対し，V1とV2の単相関が0.3 であったことを思い出そう。符号が反転しているため，解釈は真逆になってしまう。実際の単相関は正の関係であるから，条件付きであることを忘れて「V2は負の影響，V3は正の影響」と表現してしまうと，ミスリーディングなことになるからである。
また，豊田 (2017) は重回帰分析のこうした誤用を避けるために，独立変数を事前に直交化したデザインで行うコンジョイント分析の積極的な利用を提案している。我々が重回帰分析をうまく使いこなせないのであれば，そうした手法も有用であるだろう。
偏回帰係数の解釈が難しい理由の一つは，説明変数同士に相関関係がみられることにある。 特に，説明変数間の相関関係が高くなることは多重共線性Multicollinearityの問題という。この問題は，回帰係数の標準誤差がインフレを起こすことを指す。
例えば先ほどの例で，説明変数V2とV3は相関係数\(0.8\)を持っていた。この時の回帰係数の標準誤差を確認しておこう。
summary(result.mra)
Call:
lm(formula = V1 ~ V2 + V3, data = X)
Residuals:
Min 1Q Median 3Q Max
-2.59118 -0.54717 -0.03692 0.55044 2.90735
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.414e-17 2.690e-02 0.000 1
V2 -2.778e-01 4.486e-02 -6.192 8.65e-10 ***
V3 7.222e-01 4.486e-02 16.100 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8507 on 997 degrees of freedom
Multiple R-squared: 0.2778, Adjusted R-squared: 0.2763
F-statistic: 191.7 on 2 and 997 DF, p-value: < 2.2e-16標準誤差は0.0449であり，それほど大きくない標準誤差で問題がないようである。しかし両者の相関係数がより高くなり，一方が他方に線形的に従属してしまうと係数の推定値が不安定になるため，注意が必要である。
このインフレを確認するための指標がVariance Infration Factor: VIFである。Rではcarパッケージにあるvif関数に重回帰モデルを入れることでこの指標が算出される。一般にVIFが3，あるいは10を超えると多重共線性が生じており，解釈に注意が必要と言われている6。
library(car) # なければ入れておこう
vif(result.mra) V2 V3
2.777778 2.777778 幸い，今回の値はこれらの基準を下回っていたので許容範囲内である。
重回帰分析の場合は複数の説明変数があるが，これを投入するときに全ての変数を同時に投入するか，順番をつけて投入するかといった手法の違いがある。前者を強制投入法と呼ぶこともある。 順番をつけて投入する方法は，逐次投入と呼ばれる。この場合は，適合度指標などを参考に変数を追加あるいは削除して，適合度が統計的に有意に向上するかどうかを考えながら進めていく。
重回帰係数の予測値\(\hat{y}\)と，被説明変数\(y\)の相関係数\(R_{y\hat{y}}\)は重相関係数と呼ばれ，予測がうまくいっているかどうかを表す適合度の一つである。相関係数なので\(-1\)から\(+1\)までの値を取りうるが，\(-1\)は逆に完全に合致していることになるので，この相関係数の符号は大して情報を持たない。そこでこれを二乗した\(R_{y\hat{y}}^2\)を考える。これは決定係数とも呼ばれ，説明変数の分散のうち予測値の分散が占める割合を表している。7
説明変数の逐次投入は，説明変数を持たないヌルモデルから一つずつ追加していくForward Selection，全ての変数を投入してから一つずつ減らしていくBackward Selectionがある。Forwardのほうは追加することによって\(R^2\)が有意に増加するか，Backwardのほうは削除しても有意に\(R^2\)が減らないか，を確認しながら進めることになる。この方法は手元のデータに最も適した説明変数のペアを選出できる方法ではあるが，検定を繰り返していることの問題と，手元のデータ以外に一般化する時の根拠の乏しさから，用いられないこともある。
逐次投入法には別の観点からの手法もある。それが階層的回帰分析である。この手法は，重回帰分析における交互作用項の投入を検討する文脈で発展した。重回帰分析では，説明変数同士の相関がない，もしくは小さい方が望ましい。しかし，交互作用とは分散分析における組み合わせの効果を表すものであり，実験デザインによっては交互作用効果が重要な変動であることも少なくない。回帰分析と分散分析は，一般線形モデルという形で統一的に理解されるが，回帰分析でも連続的に変化する組み合わせの効果を考えることができる。交互作用があるということは説明変数間に相関があることを意味するため，回帰分析の大前提に抵触する可能性があり，その投入には慎重を期する必要がある。
こうした文脈から，まずは要因の効果を投入し，次に交互作用項を投入してモデル適合度の有意な改善がみられるかどうかを検証する手順が推奨されている。この逐次投入法を特に階層的回帰分析と呼ぶ。ここでの「階層」とは，手順が重要度順に進められていることを意味し，データの特徴に関するものではないことに注意が必要である8。
サンプルが母集団から得られた確率変数であるのだから，(偏)回帰係数もまた確率変数である。すなわち，サンプルが変わるごとに変化し，その揺らぎがある確率分布に従うと考えられる。これを確認するためには，データ生成過程をモデリングし，反復することで近似させて理解するのがいいだろう。
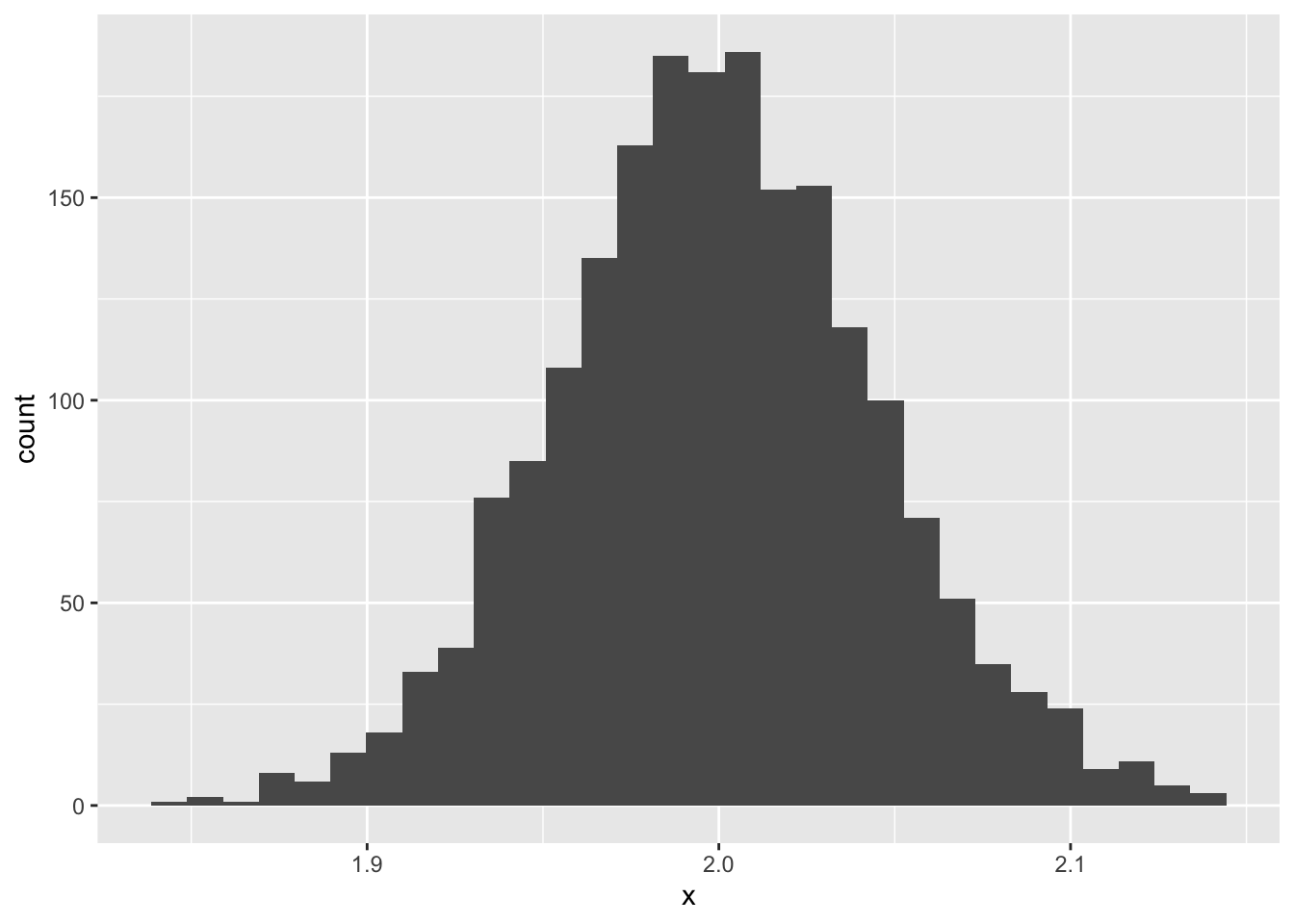
set.seed(123)
n <- 500
beta0 <- 2
beta1 <- 3
sigma <- 1
# データ生成関数
dataMake <- function(n, beta0, beta1, sigma) {
x <- runif(n, -10, 10)
e <- rnorm(n, 0, sigma)
y <- beta0 + beta1 * x + e
dat <- data.frame(x, y)
return(dat)
}
# 結果オブジェクトの準備
iter <- 2000
beta0.est <- rep(NA, iter)
beta1.est <- rep(NA, iter)
# simulation
for (i in 1:iter) {
sample <- dataMake(n, beta0, beta1, sigma)
result.lm <- lm(y ~ x, data = sample)
beta0.est[i] <- result.lm$coefficients[1]
beta1.est[i] <- result.lm$coefficients[2]
}
data.frame(x = beta0.est) %>% ggplot(aes(x = x)) +
geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
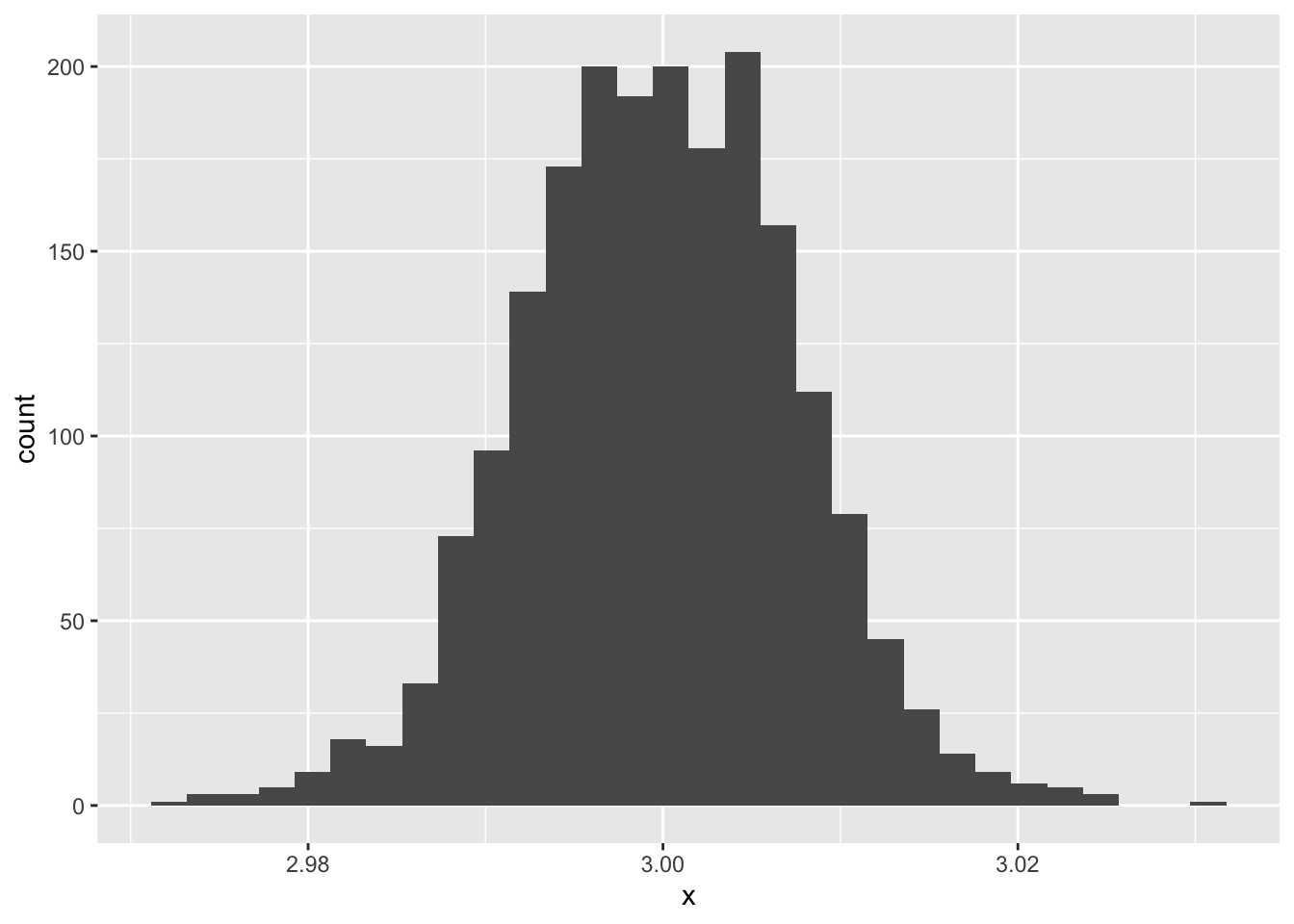
data.frame(x = beta1.est) %>% ggplot(aes(x = x)) +
geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
図から明らかなように，回帰係数も確率的に分布する。ただしその平均は理論値に近似している。
mean(beta0.est)[1] 1.999257mean(beta1.est)[1] 2.999798この分布の幅が回帰係数の標準誤差である。
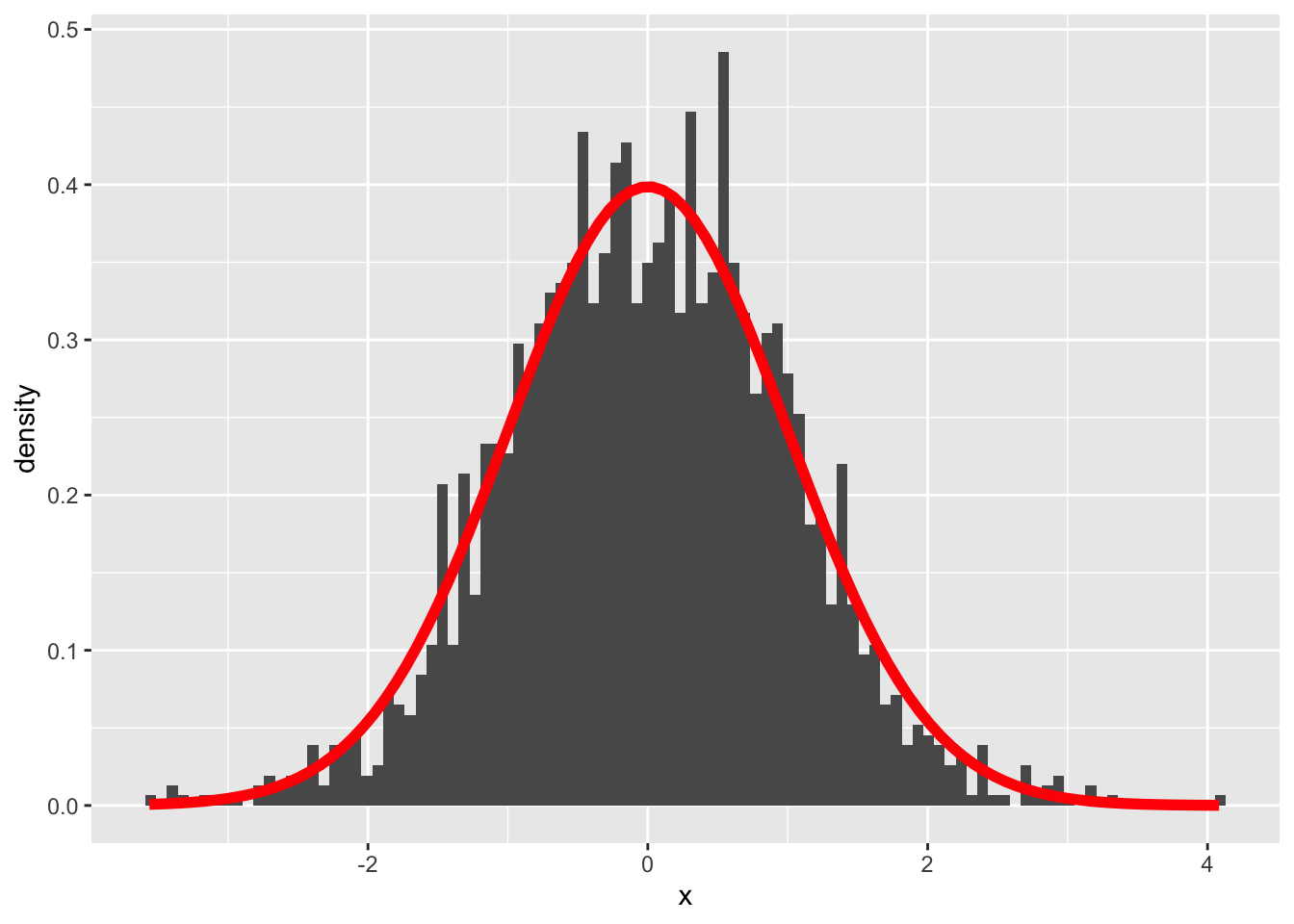
sd(beta0.est)[1] 0.04580387sd(beta1.est)[1] 0.007659277回帰係数はt分布に従い，その自由度はサンプルサイズからモデルで用いる係数の数を引いたものになる。先ほどのヒストグラムを基準化し，理論分布を重ねて描画してみることで確認しておこう。
data.frame(x = beta1.est) %>%
scale() %>%
ggplot(aes(x = x)) +
geom_histogram(aes(y = after_stat(density)), bins = 100) +
stat_function(fun = function(x) dt(x, df = n - 2), color = "red", linewidth = 2)
このt分布を用いて，係数が0の母集団から得られたサンプルなのかどうかの検定が行われる。
一方で，出力の最後にはF統計量による検定も行われていたことを確認しておこう。次に示すのは重回帰分析の例である。
set.seed(123)
n <- 500
beta0 <- 2
beta1 <- 0
beta2 <- 0
sigma <- 1
x1 <- runif(n, -10, 10)
x2 <- runif(n, -10, 10)
e <- rnorm(n, 0, sigma)
y <- beta0 + beta1 * x1 + beta2 * x2 + e
sample <- data.frame(y,x1,x2)
result.lm <- lm(y ~ x1 + x2, data = sample)
summary(result.lm)
Call:
lm(formula = y ~ x1 + x2, data = sample)
Residuals:
Min 1Q Median 3Q Max
-2.85235 -0.68275 -0.01436 0.67809 2.70488
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.996999 0.045263 44.120 <2e-16 ***
x1 -0.006453 0.007970 -0.810 0.418
x2 -0.003928 0.007795 -0.504 0.615
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.012 on 497 degrees of freedom
Multiple R-squared: 0.001893, Adjusted R-squared: -0.002124
F-statistic: 0.4713 on 2 and 497 DF, p-value: 0.6245上の例では，統計量\(F\)が，自由度\(F(\) 2,497 \()\)のもとで，0.4713であり，統計的に有意ではないと判断される(p=0.6245,n.s.)。
これは重相関係数に対する検定であり，母集団においてモデル全体としての説明力が0である，という帰無仮説を検証しているものである。この有意性検定には，説明変数の数\(p\)，サンプルサイズ\(n\)，重相関係数\(R^2\)を用いて，以下の式で用いられる検定統計量Fを利用する(南風原 2014)。
\[ F= \frac{R^2}{1-R^2}\cdot\frac{n-p-1}{p} \]
ここで右辺第一項目はCohenの効果量(\(f^2=\frac{R^2}{1-R^2}\)) といわれ，サンプルサイズ設計においてはこの指標が利用される。
重回帰分析のサンプルサイズ設計は，変数の効果の大きさ(回帰係数)が事前にわかっているのであれば，nを徐々に増やしていくシミュレーションによって行える。しかしそのようなケースは稀であり，実際には\(R^2\)の検定を用いて，ある効果量と検出力の下で，正しく検出できるサイズを算出することになる。
サンプルサイズの算出には，非心F分布を用いる。この時の非心度は，効果量\(f^2\)に\(n\)をかけたものになる。これを使ってサンプルサイズ設計をする例は以下のとおりである。
f2 <- 0.15 # 効果量
alpha <- 0.05 # タイプ1エラー率
beta <- 0.2 # タイプ2エラー率
p <- 5 # 説明変数の数
for(n in 10 : 500){
lambda <- f2 * n
df1 <- p
df2 <- n - p - 1
cv <- qf(p = 1- alpha, df1, df2)
t2error <- pf(q = cv, df1, df2, ncp = lambda)
if(t2error < beta){
break
}
}
print(n)[1] 92この設定では，n = 92以上であればモデルとして影響力がないとは言えない，ということがわかる。
重回帰分析は，人文社会科学で多用される技術ではあるが，技術が先行して理解が伴わないまま利用されているケースも少なくない。繰り返しになる点もあるが，以下に注意点をまとめておく。
y x1 x2
1 1.8685595 -4.248450 1.9997792
2 -0.5728781 5.766103 -3.3435292
3 1.0321850 -1.820462 -0.2277393
4 10.0468488 7.660348 9.0894765
5 -1.1968078 8.809346 -0.3419521
6 9.6719213 -9.088870 7.8070044 y x1 x2
1 3.586304 -0.4248450 0.132767341
2 8.599252 0.5766103 0.922713561
3 2.397115 -0.1820462 0.053684622
4 3.505236 0.7660348 0.007801881
5 6.517720 0.8809346 0.633076091
6 -1.394231 -0.9088870 -0.895346802もちろん証明できる。\(\beta_0 = \bar{y} - \beta_1\bar{x},\beta_1 = r_{xy} \frac{s_y}{s_x}\)より，\(\bar{\bar{y}} = \frac{1}{n}\sum(\bar{y} - \beta_1\bar{x} + \beta_1x_i) = \bar{y} - \beta_1\bar{x} + \beta_1\frac{1}{n}\sum x_i = \bar{y}\)である。↩︎
もちろん証明できる。\(\bar{e} = \frac{1}{n}\sum e_i = \frac{1}{n} \sum (y_i - \hat{y}_i) = \bar{y} = \bar{\hat{y}} = 0\)である。↩︎
縦軸の標準化された残差の大きな値は解釈に注意が必要な外れ値である可能性が高い。レバレッジも同様に回帰係数に大きな影響を与える値の指標であり，この図の端に位置する変数は注意が必要，と考える。↩︎
論文が早期公開された後，心理学会が主催するオンラインシンポジウムでは著者とこの論文で取り上げられた論文の著者が登場して，議論が交わされた(日本心理学会YouTubeライブ・話題の論文について著者と語るシリーズ,2021年7月2日20時-21時40分)。平日の夜という設定，早期公開版における議論であったにも関わらず，1700名近い視聴者が参加した。↩︎
2変数重回帰分析モデルで，VIFが3であれば説明変数間の相関は\(r=0.81\)程度である。VIFが10であれば\(r=0.97\)にもなる。詳しくは 小杉, 紀ノ定, and 清水 (2023) を参照。↩︎
これに対して，データの階層性(ex.学級\(\subset\)市区町村\(\subset\)都道府県)を考慮する線形モデルのことを，階層線形モデルHierarichal Linear Model:HLM という。↩︎